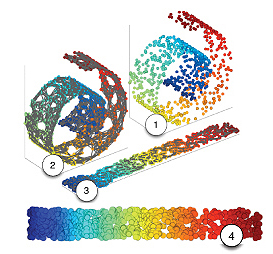Manifold Learning | Manifold Learning |
|
A discretized manifold is revealed by connecting each data point and its k=6 nearest neighbors 2. An unsupervised learning algorithm unfolds the Swiss roll while preserving the local geometry of nearby data points 3. Finally, the data points are projected onto the two dimensional subspace that maximizes their variance, yielding a faithful embedding of the original manifold 4. |
