Extreme Directions | Extreme Directions |
|
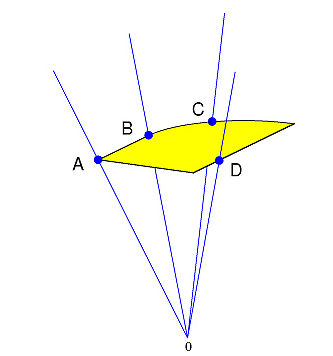
The property extreme direction arises naturally in connection with the pointed closed convex cone, being analogous to extreme point. An extreme direction of a pointed closed convex cone is a vector corresponding to an edge that is a ray emanating from the origin. In words, an extreme direction in a pointed closed convex cone is the direction of a ray, called an extreme ray, that cannot be expressed as a conic combination of any ray directions in the cone distinct from it. Extreme directions of the positive semidefinite cone, for example, are the rank-1 symmetric matrices. |
