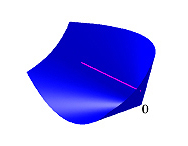
An elliptope is that convex Euclidean body formed from elements that are vectorized matrices.  Each matrix constituting an elliptope has 1 in each entry along the main diagonal and is positive semidefinite.  These matrices are also known as the correlation matrices.  The elliptope is important because some optimization problems involving positive semidefinite matrices can be restricted to the elliptope without loss of generality.  This constraint can simplify problems.  The cone of Euclidean distance matrices can be formed by manipulating an elliptope.

The early proponents of this convex body defined vertex as a point having full-dimensional normal cone.  This led to vertices only at the pointy ends of the malformed pillow illustrated.  But the more conventional convex definition of vertex describes it as any point that can be isolated by a supporting hyperplane.  This is the definition we adopt, which leads to an infinity of vertices.  Although the elliptope's relative boundary looks smooth, is is actually rough because of all the vertices. 

Above is that pillow-shaped elliptope formed from all positive semidefinite 3x3 matrices having 1 along the main diagonal.

In the example illustrated above, the elliptope is that line segment interior to the positive semidefinite cone of 2x2 matrices.

Fantope is our nomenclature named after mathematician Ky Fan.
A Fantope is the convex hull of that set comprising outer product of all orthonormal matrices of particular dimension.  The column dimension indexes a corresponding fantope.  The Fantope plays a critical role in the implementation of rank constraints in semidefinite programs.

In the example illustrated, the circular Fantope represents outer product of all 2x2 rank-1 orthonormal matrices.  The identity matrix is the Fantope comprising outer product of all 2x2 rank-2 orthonormal (orthogonal, in this case) matrices.

Read more...