Distance Matrix Cone | Distance Matrix Cone |
|
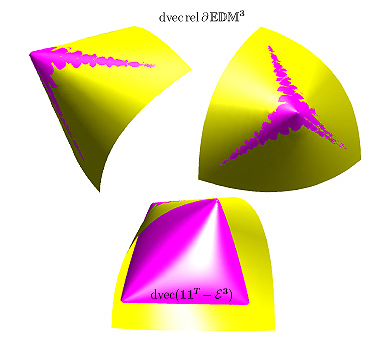
In the subspace of symmetric matrices, the set of all Euclidean distance matrices forms a unique immutable pointed closed convex cone called the EDM cone; a.k.a, the cone of Euclidean distance matrices. The EDM cone in higher dimension is the intersection of an infinite number of halfspaces about the origin and a finite number of hyperplanes through the origin. Hence the EDM cone has empty interior because it is confined to the symmetric hollow subspace. We introduce a new equality relating the EDM cone to a positive semidefinite cone; the EDM cone is on the left side of this equality while the positive semidefinite cone and two other subspaces are are the right. This is an equality between two large convex Euclidean bodies that has been overlooked in the literature and not published elsewhere. Although Isomorphisms relating the EDM cone to a positive semidefinite cone are well known, they have never led to this equality. |
