Dattorro Convex Optimization of a Reverberator
From Wikimization
| Line 11: | Line 11: | ||
To address this problem, it may perhaps be easier to begin with the simpler topology presented by [http://ccrma.stanford.edu/~dattorro/music.html Dattorro] | To address this problem, it may perhaps be easier to begin with the simpler topology presented by [http://ccrma.stanford.edu/~dattorro/music.html Dattorro] | ||
| - | in [http://ccrma.stanford.edu/~dattorro/EffectDesignPart1.pdf Effect Design, Part 1]. (Level of difficulty, for this problem in Optimization, is worthy of a Ph.D. thesis in 2010.) | + | in [http://ccrma.stanford.edu/~dattorro/EffectDesignPart1.pdf Effect Design, Part 1]. (Level of difficulty, for this open problem in Optimization, is worthy of a Ph.D. thesis in 2010.) |
Revision as of 21:29, 1 July 2010
Login required to E-mail this user.
If you do not already have an account, create one here.
mailto:dattorro@stanford.edu Jon Dattorro
Convex Optimization of a Reverberator
Given this industrial-strength topology for reverberation of audio, it is an open question to derive a method for choosing delayline lengths such that perceived decay is exponential. In layman's terms, it is difficult to choose delayline lengths that will not cause undulation in this reverberator's decay-tail in response to an impulsive input.
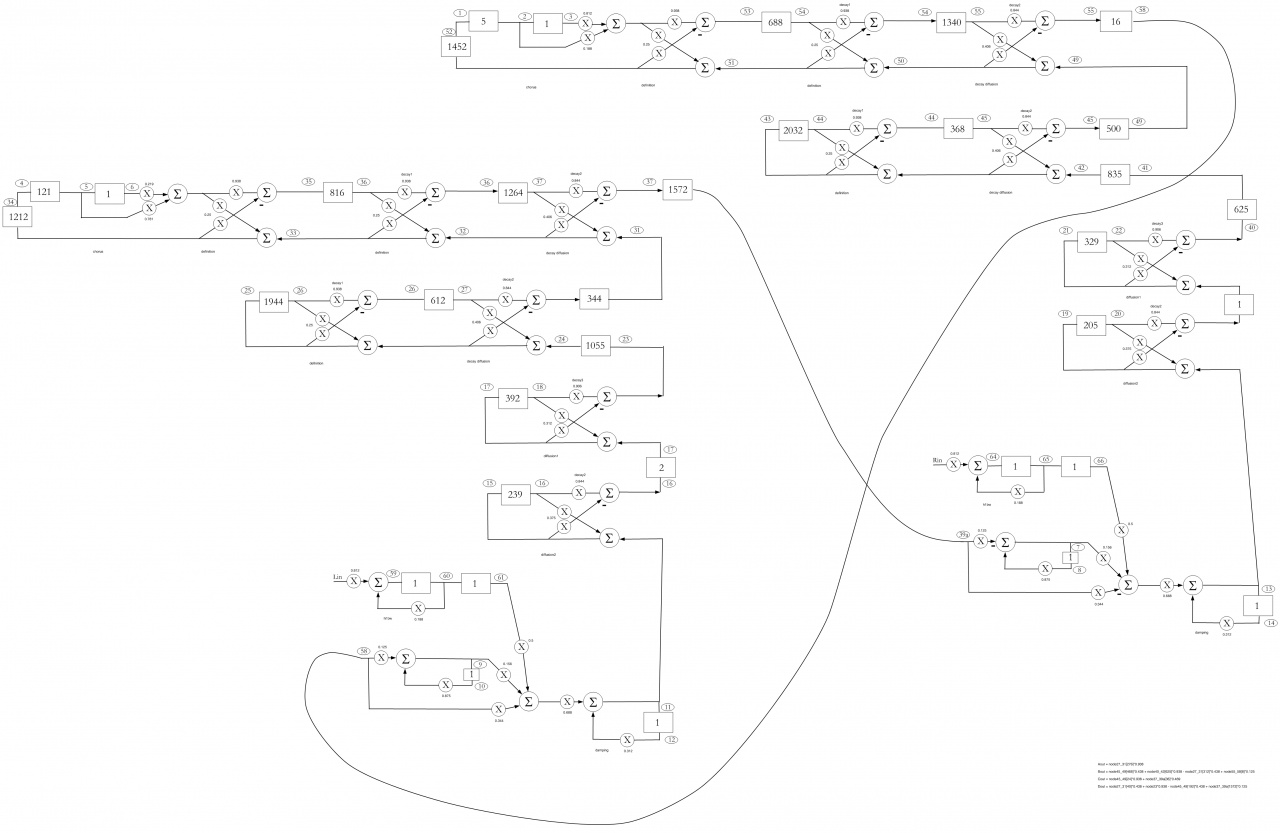
Choice of delayline length is an optimization problem because one must simultaneously insure that the network provides good musical qualities; e.g., a good reverberator should provide little coloration (input spectral change).
To address this problem, it may perhaps be easier to begin with the simpler topology presented by Dattorro in Effect Design, Part 1. (Level of difficulty, for this open problem in Optimization, is worthy of a Ph.D. thesis in 2010.)